算子
英语的算子是Operator,含义为操作、运算等等。 算子可以理解为,把一个函数变成另一个函数的东西。 函数是从数到数的映射。 泛函是从函数到数的映射。 算子是从函数到函数的映射。
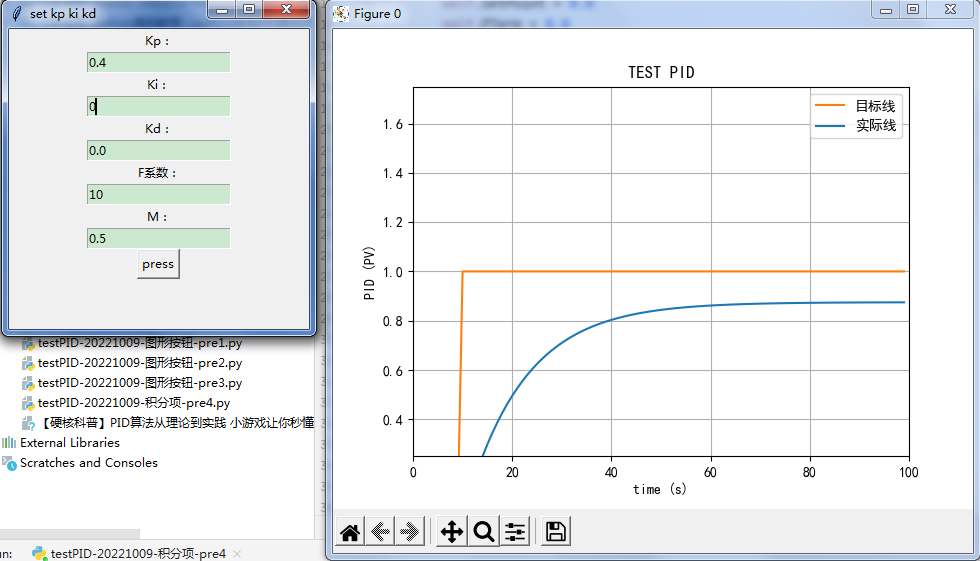
PID程序测试积分项演示
可以看出,随着积分项的引入,稳态误差被消除 [hide] 源代码1 [/hide] 尤其是中值不准的时候: [hide] 源代码2 [/hide] 积分饱和现象多产生于控制器长时间无法消除误差,导致积
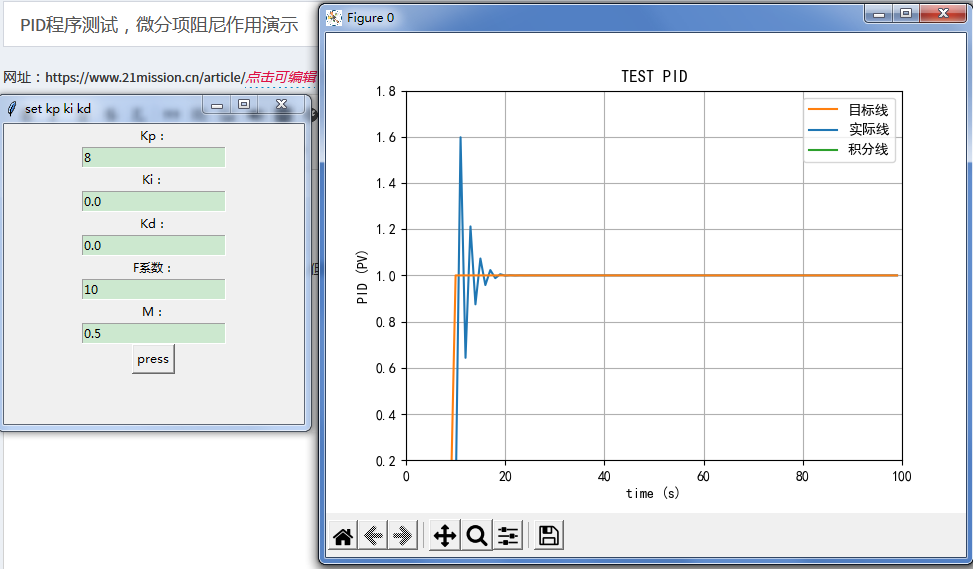
PID程序测试,微分项阻尼作用演示
可以看出,虽然首次因为初始值的问题冒冲出来,但是后面会趋于缓和(阻尼) [hide] 源代码 [/hide]
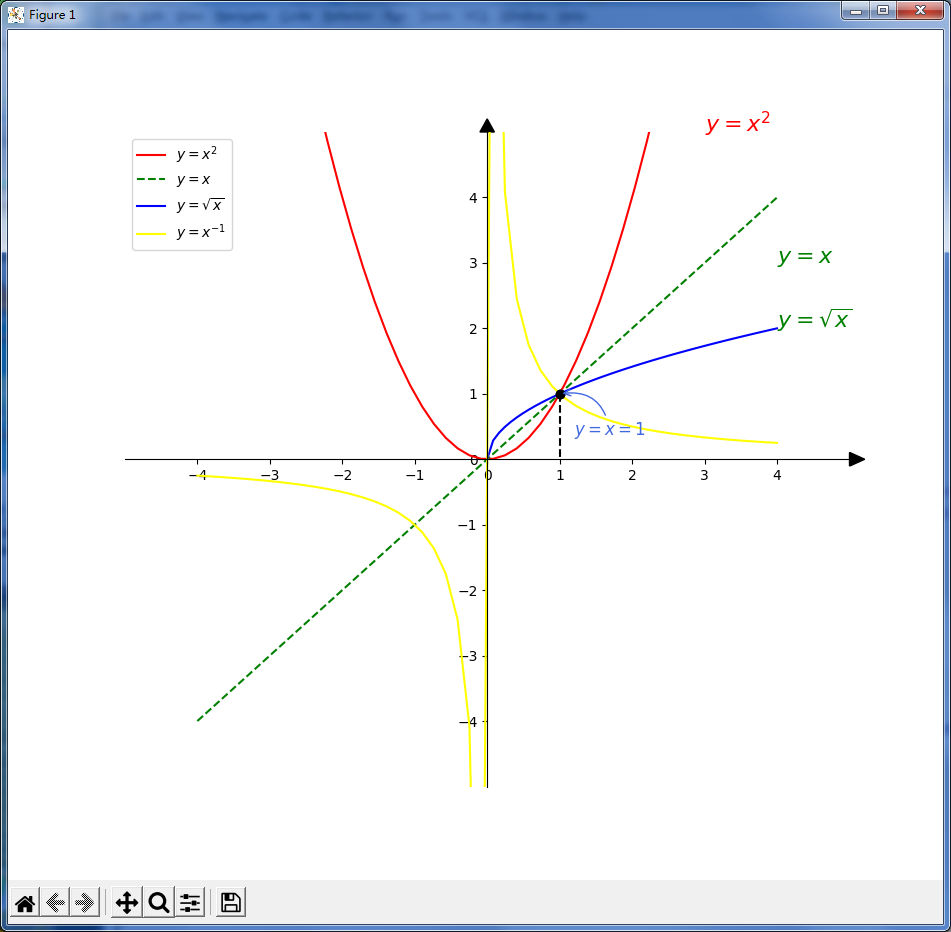
高中数学函数图像
幂函数 指数函数 对数函数 高中数学函数图像python源代码
数学入门的四条大道
1.巴塞尔问题(涉及数列、极限、代入、等价、近似、相似三角形) 2.上帝随机数(涉及线性同余、混合同余、乘同余、群论、完系和缩系、齿轮、五度相生律) 3.广义相对论之度规张量(涉及线性代数、线性变换、
完系和缩系
与模m互素的剩余类: 剩余类:用一个正数代表在 (mod n)情况下的同余集合。 比如10的[1]={1,11,21,~~~,-9,-19,~~~} 剩余类集:显然就是剩余类的集合 例如:Z10 ={
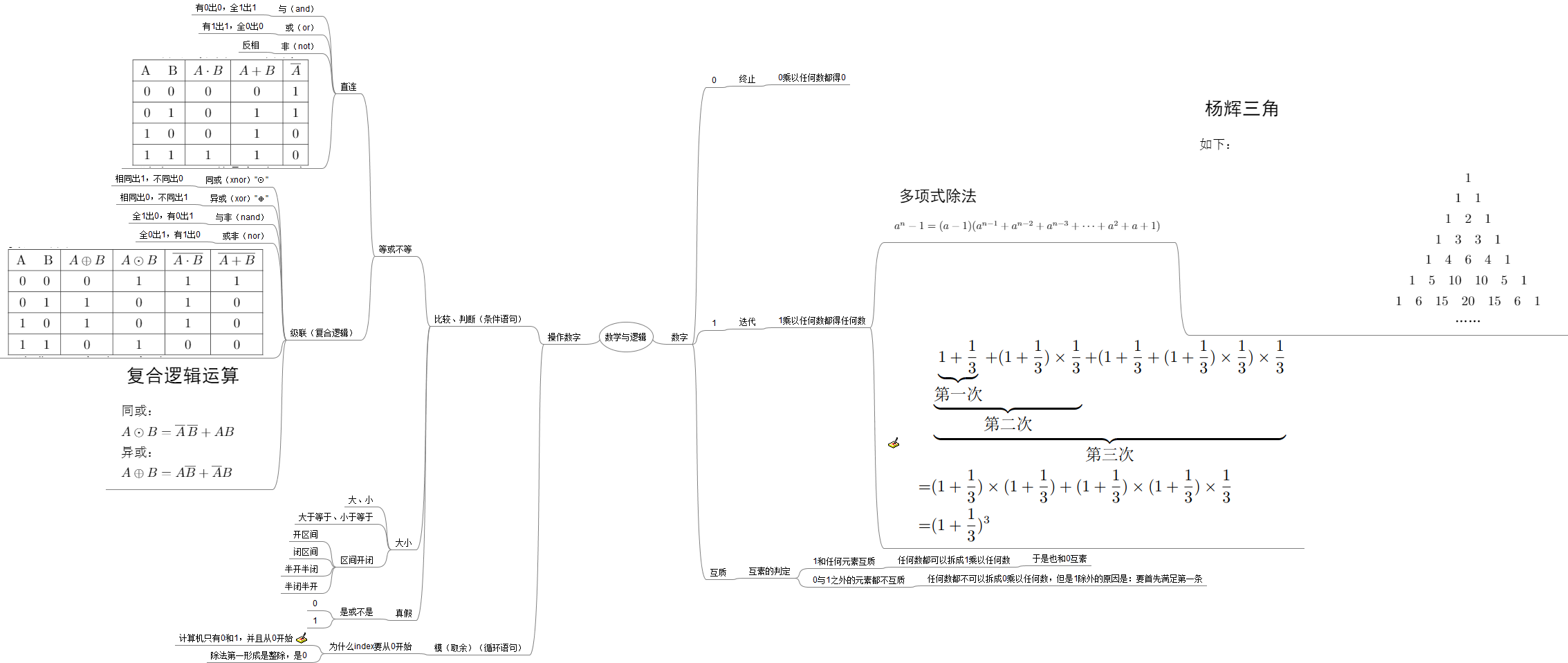
数学与逻辑(少儿编程课程)
逻辑门
多么细节的领悟LCG
意外的,用solidworks画齿轮渐开线。结合去年今日研究的线性同余产生随机数。印证了加法同余和乘法同余在两个互斥齿数上遍历的过程。奇怪的发现了欧拉函数和倍数齿轮素数时原根倍数可得模减一的相同个数的
一个数的原根
费马小定理、威尔逊定理和欧拉定理 原根的概念、性质及其存在性
Hull-Dobell Theorem
relatively prime 英 [ˈrelətɪvli praɪm] 互质; 互素 prime factors 英 [praɪm ˈfæktəz] 质因数 primitive root 英 [ˈ