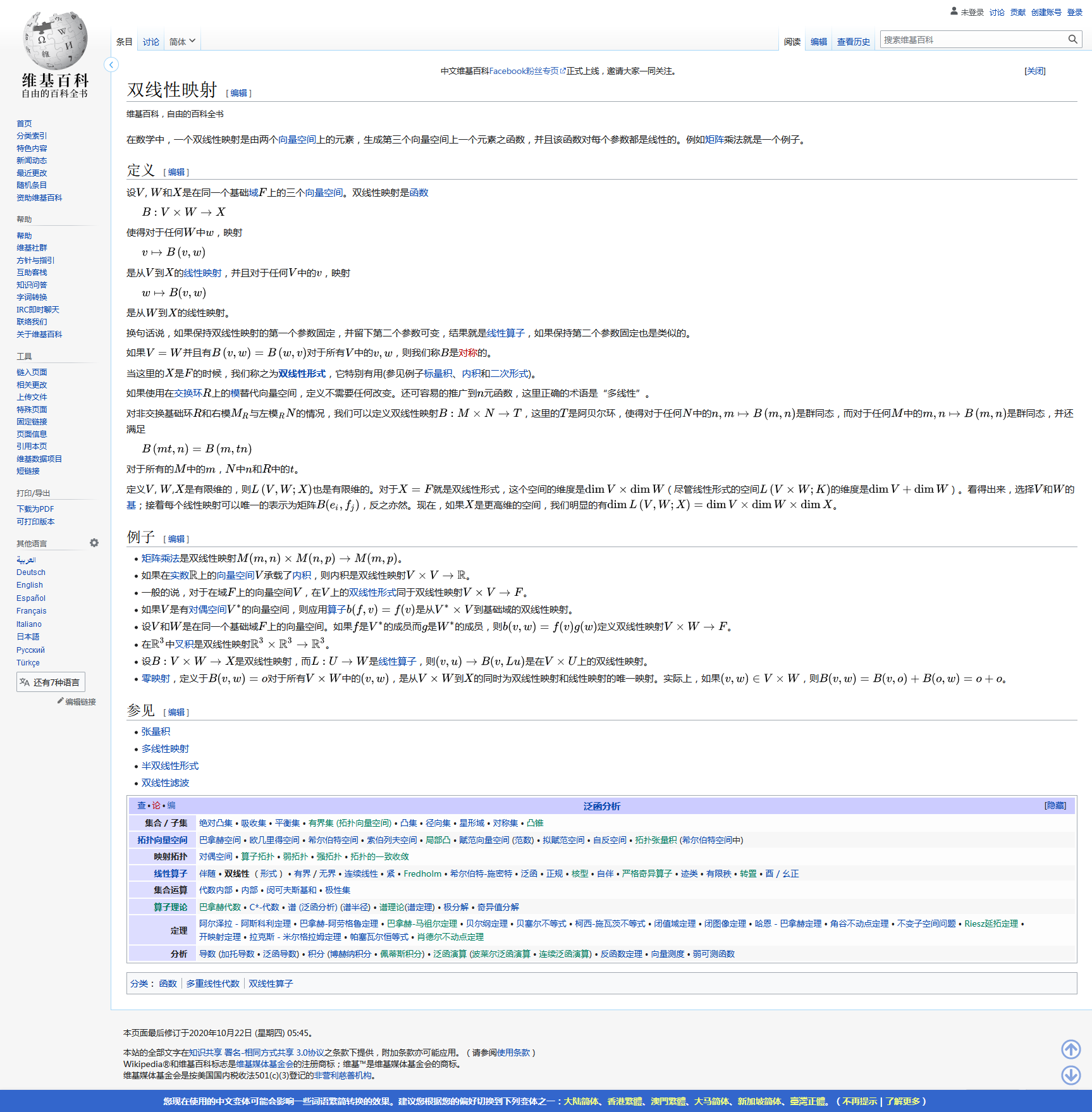
双线性性才能用乘法分配律去证明余弦定理
内积证明余弦定理:
投影的平行证明
把太阳光看成平行光,那么大地方向上获得直立的影子,就是直立向量在倾斜方向上的投影。 这里需要解释的就是平行光。 如果取一米的光线,离太阳越远,则同等平行距离内,两条光线的两端距离之差将越小。这由近大远
相似三角形
简介 三角分别相等,三边成比例的两个三角形叫做相似三角形(similar triangles) 相似三角形是几何中重要的证明模型之一,是全等三角形的推广。全等三角形可以被理解为相似比为1的相似三角形。
初中数学思维导图人教版7~9
人教版初中思维导图
0为什么不能做除数
从代数来说: 1. 乘法是快速的加法。减法是加法的逆运算。除法是乘法的逆运算。 2. 0乘任何数都等于0.乘法有交换律。 3. 当结果为0,除数为任意数时,被除数都是0. 4. 当结果为0,除数为0时
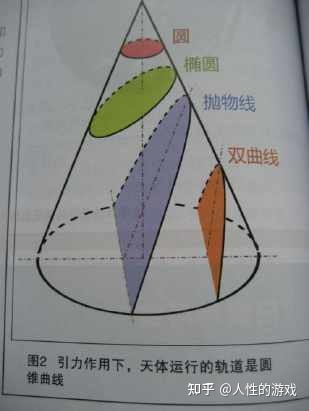
引力作用下,天体运行的轨道是圆锥曲线
与母线平行的是抛物线
两点之间线段最短vs两点确定一条直线
人教版初中数学七年级上册教材4.2 直线、射线、线段中有这样的论述: 两点确定一条直线。 剑桥大学教材中有这样的争论: “直线”的流行定义是“两点之间的最短距离”,这是英语中为数不多的通用数学术语之一
点法式、点斜式、两点式、截距式
直线的方程,有点斜式、两点式、截距式 平面的方程,有点法式、一般式、截距式 由圆锥面(一条直线绕着与其相交的另一条直线旋转一周可得),在三维上被平面截面,相交的曲线为二次曲线,分为:圆、椭圆、抛物线、
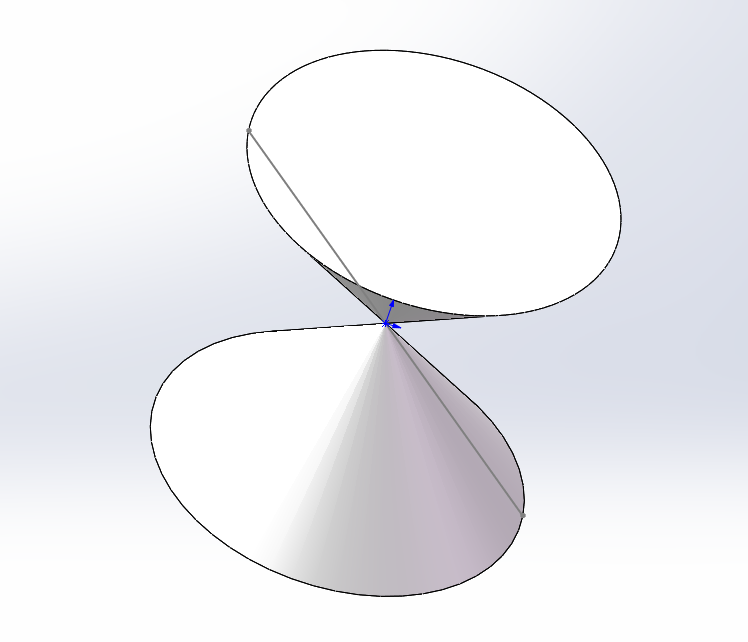
圆锥曲线
两个点可以确定一条直线。 到两个点的距离之和是定值的点,连起来是椭圆。 到两个点的距离之差是定值的点,连起来是双曲线。 到一个点和一条直线的距离相等的点,连起来是抛物线。 一条直线、绕另一条与它相交的
如何理解矩阵特征值
对于方阵而言,矩阵不会进行维度的升降,所以矩阵代表的运动实际上只有两种: 旋转 拉伸 没有投影、投射