视角的转换(少儿编程课程)
如何解决歧义问题? 在不同的人的视角下,看到的事物的不同方面,就会产生不同的理解。但是就像物理定律。不管是在地球上还是在月球,不管是在过去还是将来,不管是在哪一个平行世界,都会有重力势能、都会有动能。
0和1(少儿编程课程)
地理中,在地球上南北回归线之间的温度带是热带,北回归线和北极圈之间是北温带。 在我们所处的北温带,影子在正午会达到最短。在热带的正午,竖一根杆子,杆子有可能没有影子。 我们把没有影子的时刻定义为太阳垂
线性代数的本质:本质、以及第15集中的公理-线性代数十大法则
线性代数十大法则 线性变换: 直线在变换后仍然保持直线,不能有所弯曲(包括每个小网格的对角线延长线不能弯曲),我理解为空间匀称(各向平(间隔)直(无波动)) 原点必需保持固定 什么是线性,不能升维,不
巴塞尔问题之一、倒数勾股定理(少儿编程课程)
上一次我们求圆周率,还是上一次。 巴塞尔问题是一个著名的数论中的级数问题,问题是:求出自然数平方的倒数之和。这个问题首先由皮耶特罗·门戈利在1644年提出,由莱昂哈德·欧拉在1735年解决。由于这个问
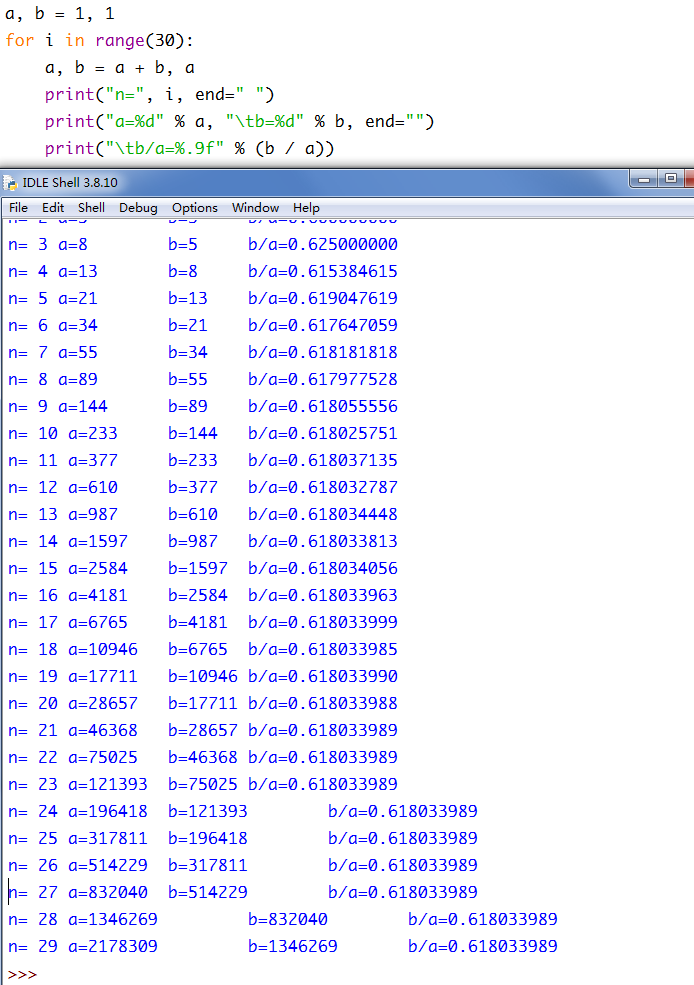
有趣的迭代(少儿编程课程)——连分数开根号、开方
黄金分割是一个数, 黄金分割是一个小数, 黄金分割是一个无限小数, 黄金分割是一个无限不循环小数。 一般用φ来表示黄金分割数。 我们可以用斐波那契数列,循环30遍,找到这个黄金比例。 也可以用无限连分
设计一款教具,演示同一圆内等弧所对应的角相等(少儿编程课程)
首先,想到有意思的玩法是: 以两点之间固定锐角的木楔子可以画出一个圆的大部分。 找刚才角度的两个木楔子并在一起嵌入这个圆中,两边相等时可以找到圆心。 然后开始设计教具。 第一版是这样的: 第二版是这样
最小公倍数、线性同余(少儿编程课程)
最小公倍数是同一起跑线,不同的步长。相同的落点,在一条无限的跑道上。 线性同余是不同的起跑线,在循环往复的圈圈中,相遇。 模运算、线性同余、齿轮、分数(有理数) 数论中的重要概念。给定一个正整数m,如
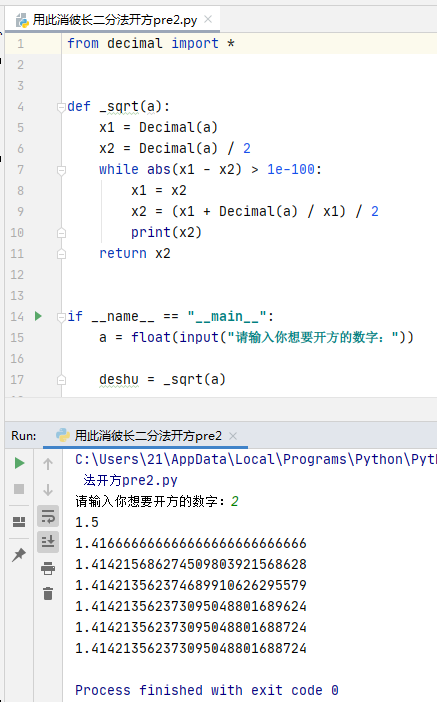
牛顿迭代法开平方(少儿编程课程)
理论部分参见——链接
从数论上讲,为什么对称会导致循环
从数论上讲,为什么对称会导致循环
为什么0不能做除数
这是一个关于数学基础的好问题。让我从几个层面来解释为什么 0 不能做除数: 核心原因:代数矛盾 假设 0 可以做除数,设 a÷0=b (其中 a≠0 ),根据除法的定义,这意味着: b×0=a 但我们