导数6:导数与微分的历史,顺便总结林群、张景中两院士的(假传万卷书,真传一案例)
4860 2022-03-24 11:10 2024-06-08 12:03
微积分发展史
先有的导数还是先有的微分?
按照课本的顺序,是先讲极限,再讲导数,再讲微分,然后是不定积分、定积分、微分方程
而实际历史发展却是先有的微分再有的导数。
牛顿和莱布尼兹各自独立发明了微积分。
他们在解决曲面下面积的时候把导数的定义确定下来了。
曲线下的面积在微积分出现之前是一个很复杂的问题,微积分求解的主要思想是把曲线下的面积划分成了无数个矩形面积之和。
这里我用python程序模拟了游戏中小人加速运动的程序。这和画圆采用步进法还是围点法异曲同工。都是多边形边数越多越接近正圆。
当t=1/100时:
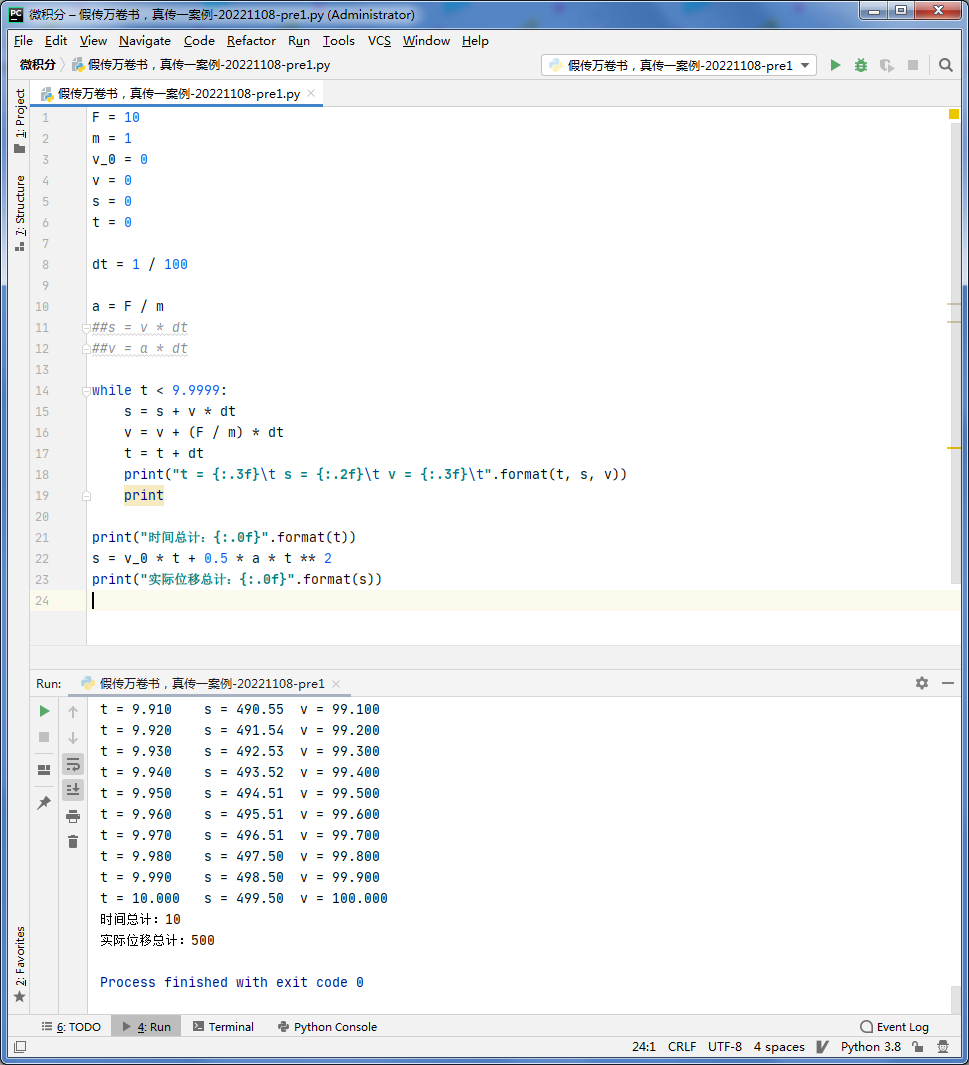

当t=1/10时

当t=1时

代码部分:

无穷小量是建立微积分的基础,莱布尼兹介绍微积分的论文就叫做《论深度隐藏的几何学及无穷小与无穷大的分析》。在当时的观点下,无穷小量到底是什么也是有争论的
导数的古典定义就是曲线的割线,可以反应曲线的平均变化率,也就是说这一段大概总的趋势是上升还是下降,上升了多少,但是并不精确。而有了切线,我们就可以精准的定义变化率。此时dx和dy被称为x和y的微分,都为无穷小量,所以导数也被莱布尼兹称为微商(微分之商)。
当时无穷小量导致的麻烦就是两点才能确定一条直线,而切线定义在初始点上,在它的发展方向上,也就是右侧增量邻域。那个小小的一步到底有多小,是有极大争论的的。近乎重叠的说法导致微积分的基础不牢固。x平方的导数计算中,dx先是在约分中被约掉,然后又在加法中被忽略,就是说,先被当作了非0的量,又被当作了0,这就是大主教贝克莱(就是在高中政治书被嘲笑的唯心主义的代表)所攻击的像幽灵一样的数,一会是0一会又不是0。无穷小量和无穷小量相除为什么可以得到不一样的值?难道不应该都是1?
无穷小量还违反了阿基米德公理(对于任何正实数 a 及 b,即使 a多么小,或是 b多么大,也必定存在自然数 n,使得 a n > b 。这公理的粗略意义是,数字系统不存在具有无穷大或无穷小性质的元素),这个才是更严重的缺陷,康托尔证明过,如果阿基米德公理被违背的话会出大问题。
200年后(19世纪),基于极限重建微积分,极限概念清晰之后才得到解决。用极限重新严格定义了导数,已经脱离了微商的概念,此时,导数应该被看成一个整体。
此时
历史上原来是先定义了微分再有的导数,现在却是先定义了导数再有的微分。
1. dy=f′(x)Δx,这是dy的定义。
2. 我们令y=x=>dy=1Δx=>dx=Δx,这个是dx的定义。
3. 最后我们可以得到dy=f′(x)dx=>dy/dx=f′(x)
dy=f′(x)dx表明微分是个函数,不是一个数,而dx=Δx也是个函数,不是一个数。重点!!!:微分是用线性函数去逼近原函数。
而此时导数成为了两个函数的比值在某点上的取值,在某一点上就是对应的一个固定值。而导函数的值随着x的选点不同,取值也不同。导数此时又可以被称为微商了。
导数是导数

导函数是导函数

再说院士们的假传万卷书、真传一案例,
非常经典的案例,但是称之为第三代微积分也就过了。因为大道至简,无可辩驳的极限,远比小变化乘以短时间说的明白。
这个案例用简单来推出复杂,是递进的,但是又让你忽略了其中小变化带来的影响,当你看到大变化时,你就知道这个越来越小的变化,越来越细致的约束,正是近似的本质。
案例的基础是:匀速下:路程=速度*时间
匀加速下:路程=平均分的时间下,速度*时间的和
最后看出,每小段时间,如果截取的越小,那么越接近真实路程。这就是通过积分来学习微分。而速度除以时间则是加速度这个小变化。
路程函数在时间为0下的泰勒展开f(t) = f(t0) + f'(t0)(t - t0) + f''(t0)/2! \cdot (t - t0)^2
其中f(t0) = 0初始点路程为0, f'(t0)是初始时刻的初始速度, f''(t0)/2!是加速度,因为是匀变速,所以恒为a,三阶导为0,因为是匀变速,加速度不变了。
这个函数的第二项,也就是vt,这个速度乘以时间的函数下的面积,也就是积分速度关于时间的函数,可以得到路程函数的值,路程函数也就是速度函数的原函数。
这里有一点是经常让人忽略或者被人误导的。就是函数值是关于自变量的一个映射,有人说这里的f是位移函数,其实不准确,说是路程函数就比较准确。区别在于,位移给人的印象自变量是位置,如果是直线运动,那么x坐标变化,位移也就变化。但是不是因为坐标变化,而是因为时间变化,坐标才变化。这里坐标并不重要,完全可以舍弃。路程函数的值仅与时间挂钩。自变量是时间,并不是坐标。才有了关于自变量德尔塔x

全部评论