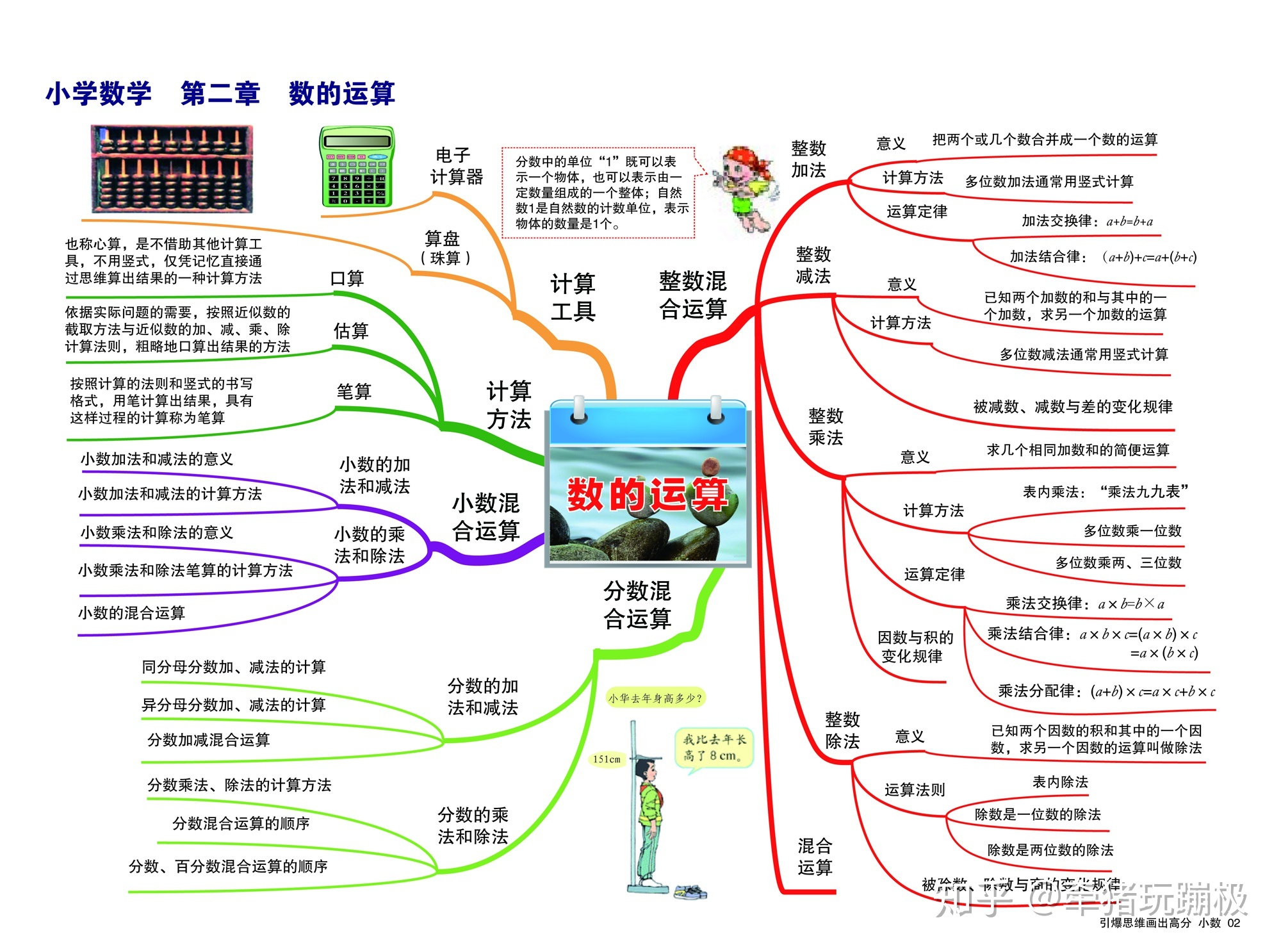
数学的主动与被动
小学中,弱化加数、乘数的顺序。所以只有减法有被减数减去减数等于差。被除数除以除数等于商和余数。
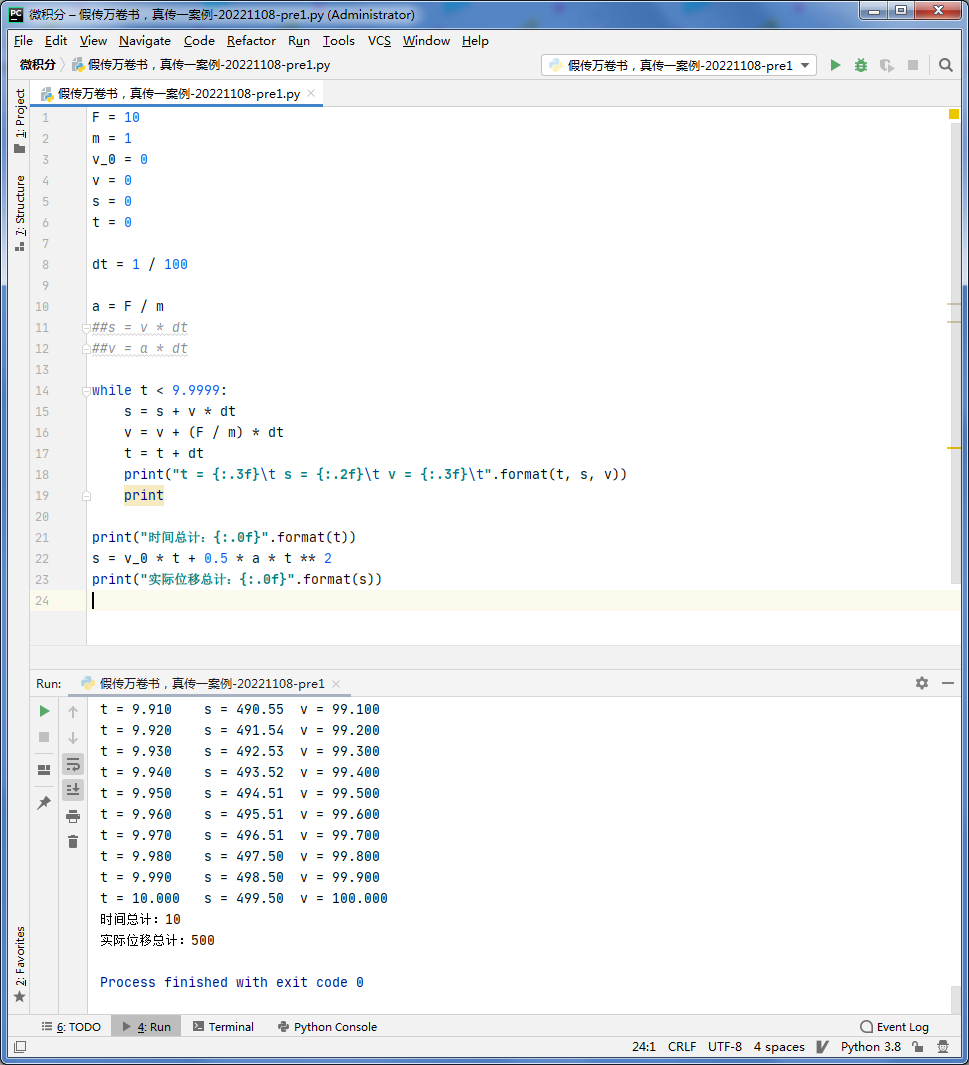
导数6:导数与微分的历史,顺便总结林群、张景中两院士的(假传万卷书,真传一案例)
微积分发展史 先有的导数还是先有的微分? 按照课本的顺序,是先讲极限,再讲导数,再讲微分,然后是不定积分、定积分、微分方程 而实际历史发展却是先有的微分再有的导数。 牛顿和莱布尼兹各自独立发明了微积分
功和能量的差别
功是过程量——当我们说到某个功时,一定是指某个物体在某个过程中因受到某个力而产生的这个功。所谓过程就是指某段时间和某段位移。功的三要素是:1)存在某个作用于某物体上的外力,2)该物体发生了一段位移,3
操作系统CPU调度三台图
进程三态:运行状态、就绪状态、堵塞状态。三态转换规则,就绪状态的进程因为调度进程运行状态,运行状态因为时间片用完而进入就绪状态,因为I/O请求而进入堵塞状态。I/O完毕后进入就绪状态。 创建完毕直接进
理解、领悟是一种能力
除去注意力是否能够保持集中。能否花够一万小时去变成某个专业的成功者。那么领悟能力、理解力的强弱,基于见识、眼力、积累。也基于天赋。 前面说到兴趣爱好是最好的凝聚注意力的方法。如果你的探索欲、求知欲特别
Latex 各个章节加Label引用的问题
有时需要在文章中引用某个章节如section 3.1,我们希望“3.1”能够直接连接到指定的章节,这就需要对 \section{....}或者\subsection{....}添加label,格式如下
微积分教学(五):椭圆面积、椭球体体积
椭圆面积、椭球体积 椭球任意切一刀都是椭圆
微积分教学(四):球体体积、球体表面积
球体体积、球体表面积 把半径为r的球想像成由很多空心球壳组成的物体,且每个球壳的厚度为无限薄。假设每个球壳都可以展开成平面,将这些平面按大小顺序叠起来,就可以得到一个底面积为4πr^2(球的表面积),
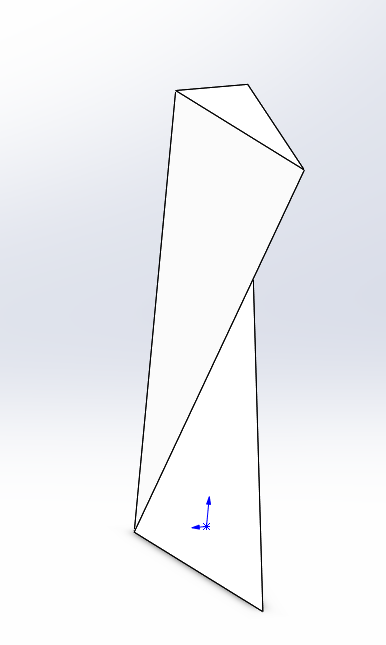
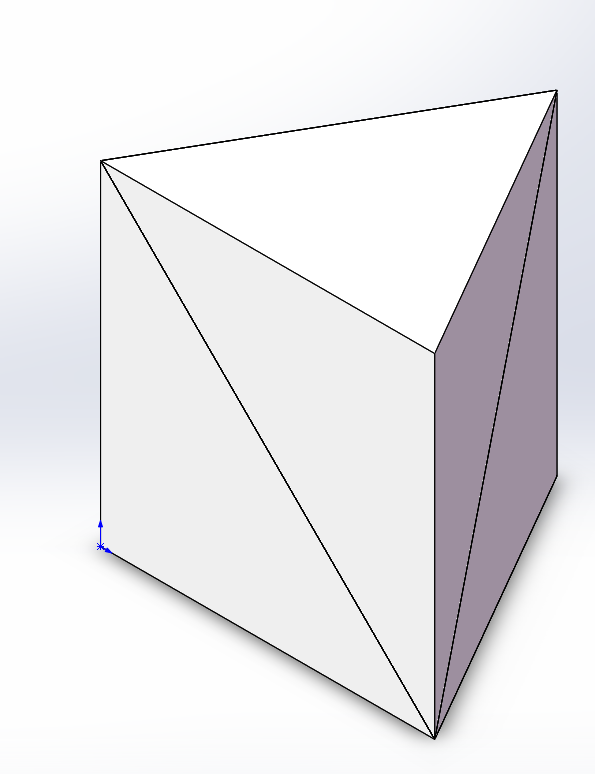
微积分教学(二):菱形体体积
斜砍一刀,砍下的部分是原来的三分之一,再砍一刀,砍下的部分是原来的三分之一,剩下的部分是最后的三分之一。