led就是二极管,没有电阻,怎么分压?
LED(发光二极管)在电路中确实具有电阻特性,尽管它不是传统意义上的电阻器。LED有一个正向电压(VF),这是它开始导电并发光所需的电压。当LED导电时,它会有一定的正向电流(IF)通过它。LED的分
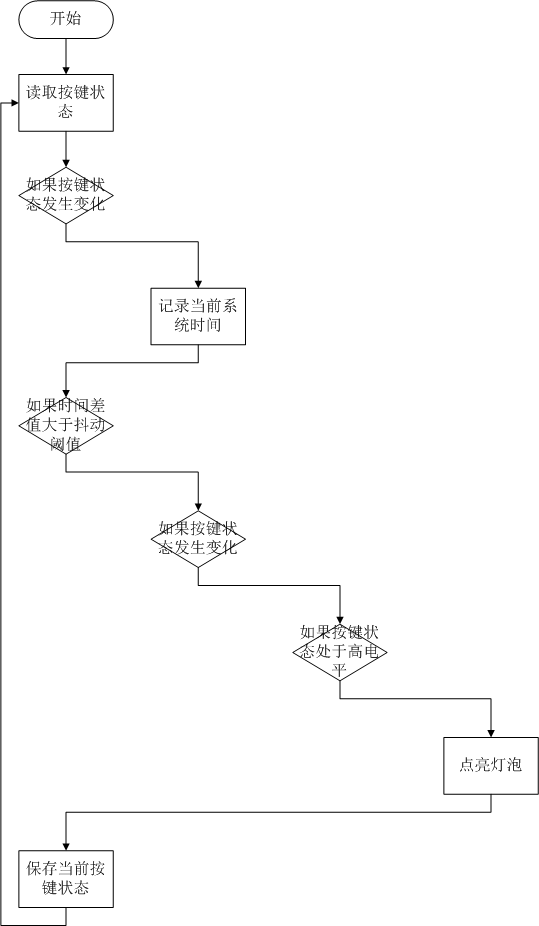
arduino按键防抖动
在Arduino项目中,按键防抖动是一个常见且重要的问题。由于机械和物理原因,按键在按下时可能会产生快速的多次开关状态变化,这种现象称为“抖动”。为了防止这种抖动导致的误操作,可以采用以下几种方法:
switch case是按顺序还是并行的。和if相比有什么区别
在编程中,`switch` 语句和 `if` 语句都是用于条件分支控制的,但它们的工作方式和使用场景有所不同。 1. **`switch` 语句**: - `switch` 语句通常用于多个条件分支,
smartknob状态机
用状态机优化下面代码 if (reading >= lower - (upper - lower) && reading < upper + (upper - lower)
如何查看显卡型号
查看显卡型号的方法因操作系统而异。以下是在不同操作系统中查看显卡型号的常见方法: ### Windows 系统 1. **使用设备管理器**: - 右键点击“开始”按钮,选择“设备管理器”。 - 展开
c语言全局变量需要static修饰吗?
在C语言中,全局变量不需要`static`修饰符。全局变量是定义在函数外部的变量,它们在程序的整个执行期间都是存在的,并且可以被程序中的任何函数访问(除非它们被限定在某个文件中,并且没有在其他文件中声
c语言变量在函数内和变量在函数外有什么区别
在C语言中,变量的作用域和生命周期是由它们定义的位置决定的。变量可以在函数内部定义,也可以在函数外部定义,这决定了它们的作用域和生命周期的不同: 1. **局部变量(函数内定义)**: - **作用域
c语言为什么要有有头文件
c语言为什么要有有头文件 在 C 语言中,头文件有以下重要作用: 一、代码复用 1. 头文件中可以包含函数声明、宏定义、结构体定义等内容,这些可以被多个源文件复用。例如,在多个源文件中都需要使用同一个
C语言的声明、定义、赋值、初始化
在编程中,特别是在使用C或C++这类语言时,"声明"(Declaration)和"定义"(Definition)是两个非常重要的概念,它们在处理变量和函数时有着
如何增加右键用vscod打开文件夹
右键菜单加入vscode 要在Windows系统中增加右键菜单选项,使用Visual Studio Code(VSCode)打开文件夹,你需要通过修改Windows注册表来实现。以下是详细的步骤: