世界的底层逻辑提示次,挑主要的说,比如:对称、群、平衡、惯性、熵增,还有什么?
下面这份“底层提示词”清单,只挑那些真正跨学科、跨尺度、几乎像空气一样到处出现的概念,按“一句话就能唤醒直觉”的标准给出。你列的对称-群、平衡、惯性、熵增已在内,其余不再赘述。 对称 → 群 任何“做
关于量子理解
我:量子是一个抽象概念和光子、电子、质子、原子不是一个概念,也和物质是否可分不是一个概念。因为都带一个子,所以让中国人产生了误解。而能量量子化则是量子的起源,之后有了量子力学、量子场论对应描述的是叠加
docker如何清理过程镜像
[root@iZ2zed4vmulmu2gioymytpZ volc-voice-web]# docker images REPOSITORY TAG IMAGE
光在传播过程中遇到原子阻挡,发生散射,光子已经不是原来那个光子了?
光在传播过程中遇到原子阻挡,发生散射,光子已经不是原来那个光子了? 这是个非常深刻的问题,涉及光子身份与散射机制的本质。 简短回答:是的,严格来说,散射后的光子已经不是“原来那个光子”了。 为什么这样
《卿卿日常》中九川设定
《卿卿日常》把天下拆成九块“川”,每川对应一种极端化的地域+文化标签,本质是把中国各省的刻板印象做二次元放大,再塞进“女选男”的联姻体系里,方便编剧快速立人物、造冲突。九川设定如下(按剧中出场频率排序
介绍费曼路径积分和光
费曼路径积分(Feynman Path Integral)是理查德·费曼提出的一种量子力学表述方式,它用“所有可能路径的叠加”取代了传统的“粒子沿单一轨迹运动”的经典观念。其核心思想是: 粒子从A到B
以光的速度看同向的光,会看到光子静止吗?反向呢?
以光的速度看同向的光,会看到光子静止吗?反向呢? 这是一个非常有趣、也很“相对论”的问题。 先说结论: 以光速“看”同向的光,不会看到光子静止; 反向的光也不会“看起来”静止或慢下来; 实际上,从光子
从测不准原理到熵增
“测不准原理”更准确的名称是不确定性原理(Uncertainty Principle),由德国物理学家维尔纳·海森堡于1927年提出,是量子力学的核心概念之一。 一、原理表述 对任意微观粒子,位置的不
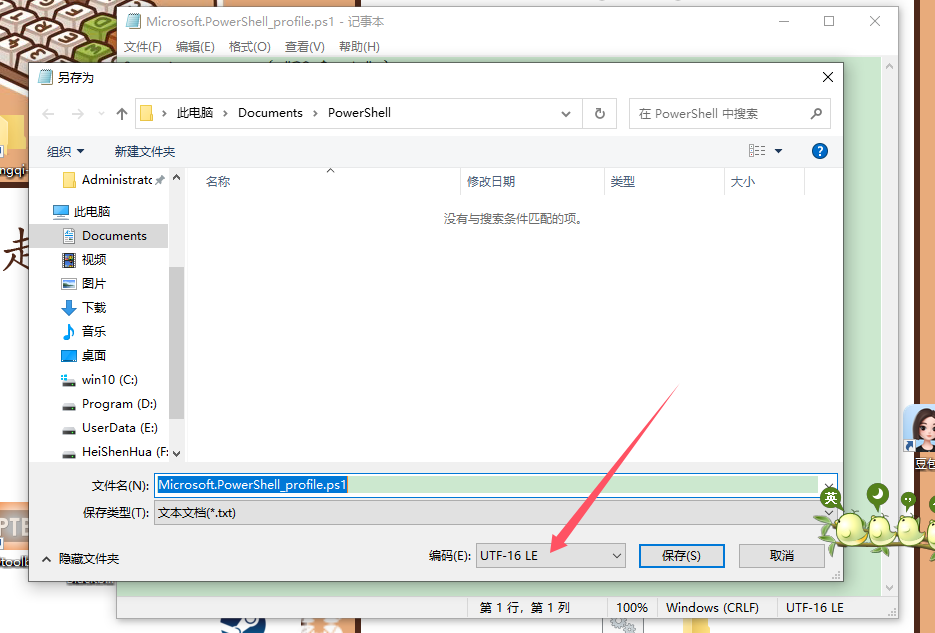
Windows Terminal如何用scoop安装?
用 Scoop 装 Windows Terminal 只需两条命令,但第一次用的人常卡在「找不到包」——因为 Windows Terminal 不在默认 bucket,而在 extras。完整步骤如下
不用winget,选用Scoop如何安装powershell7
用 Scoop 装 PowerShell 7 只要两步,全程不用管理员权限,装完就能在 PATH 里直接多出一个 pwsh 命令。 确保 Scoop 已安装(没装就执行下面一行) powershell