当我们使用地图软件输入起点和终点之后，一个按钮就可以获得从A地到B地的乘车方案。例如：

我想从八角游乐园到航天城。那么地图将会给出5种换乘方案

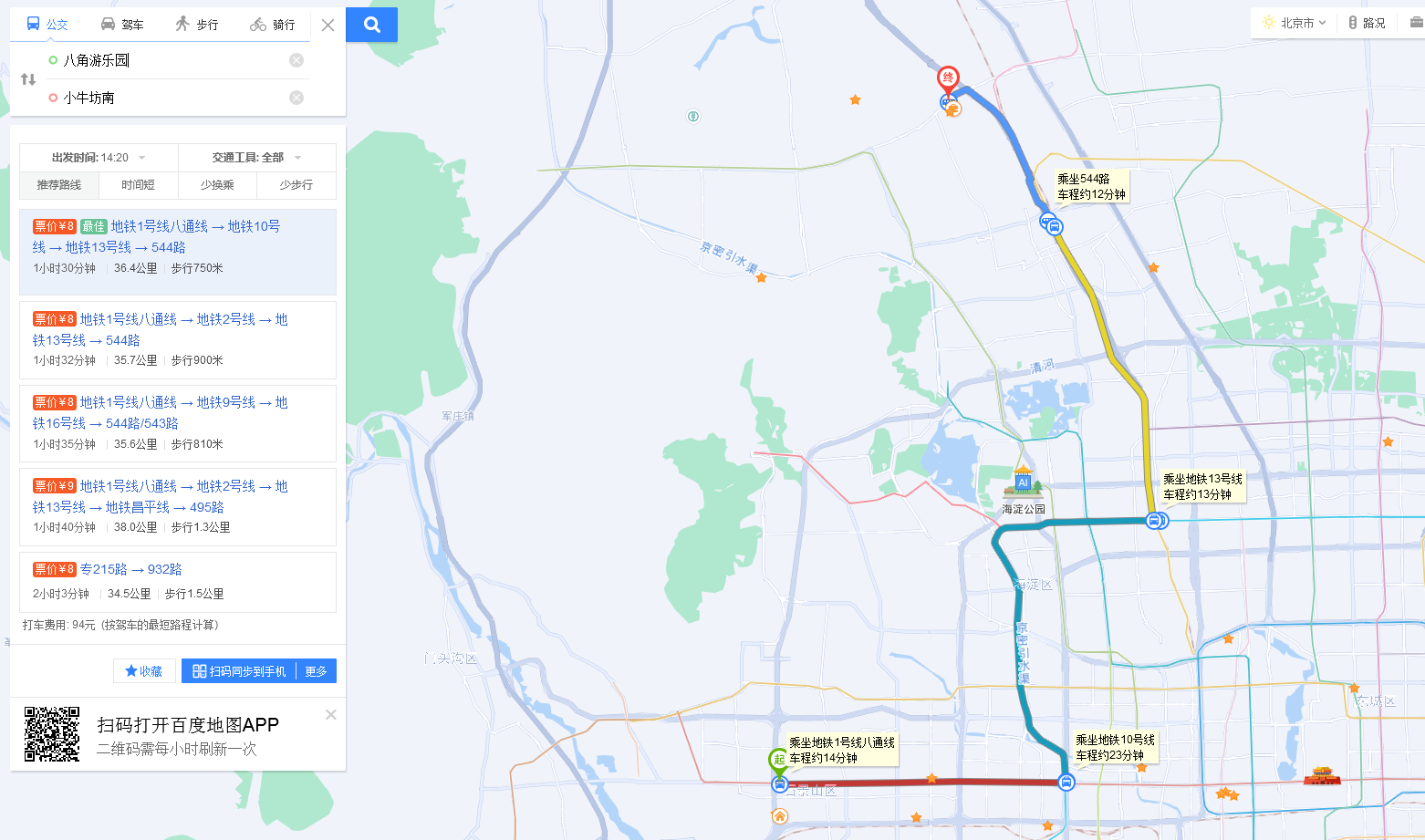
计算机是如何算出合适的线路呢？可以看到方案选项中有“时间短”、“少换乘”、“少步行”等，地铁因为其独特的密闭线路、稳定的运行时间等特点，不会有堵车的情况，所以站数越少，用时也就越少。但是综合因素中，有的老人需要少步行、天热就更希望多坐地铁少坐公交，而有时北京有大型活动、或有疫情封控的时候，还需要考虑地铁甩站的情况。坐公交就需要考虑堵车、红绿灯、发车频次等因素。同学们你们能想到的还有什么因素会影响我们出发和到达之间的时间呢？

首先让我们认识两位科学家：

迪杰斯特拉算法(Dijkstra)是由荷兰计算机科学家狄克斯特拉于1959年提出的，因此又叫狄克斯特拉算法。是从一个顶点到其余各顶点的最短路径算法，解决的是有权图中最短路径问题。迪杰斯特拉算法主要特点是从起始点开始，采用贪心算法的策略，每次遍历到始点距离最近且未访问过的顶点的邻接节点，直到扩展到终点为止。

Floyd算法又称为插点法，是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法，与Dijkstra算法类似。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。

简单说，D算法，就是固定起点之后，每次增加一个未知点入伙已知点的大家庭，算出起点经历已知点，到未知点中加和最小的那一条路。

F算法，就是逐渐增加两个点之间的介入点，更新每两个点的最短路径，不断保存每两个点的最短路径，不断更新每两个点在有新的中间点出现后最短路径的变更情况。最终把所有的点都介入完毕，也就得到了两两之间最短的路径。

首先我们标出所有的换乘站：

我们用英文字母来代替站名：

我们把每个站到另一个站需要停靠的次数用表格的形式展现出来：

在计算机眼中看到的信息就是矩阵。当我们用F算法进行邻接矩阵运算时，就会出现下面的过程：

一个邻接矩阵就让我们见识了两大算法思想的厉害，想学习四大算法思想吗？

《与孩子一起学编程》课程用四大算法思想、矩阵思维引导孩子如何观察问题、处理问题。用科学的打字方法、高维的数学认知，有逻辑有铺垫的语文表达，串联起基础学科的知识点。同时使用必备的英语软件操作环境固化基础英语单词，让孩子在日常操作中轻易读懂英文常用说明书。有兴趣的家长可以同孩子一起学习哟~

如果事件发生的可能性可以在有限次被穷举，那么我们就可以用矩阵来运算所有的出路。1997年5月11日，国际象棋世界冠军卡斯帕罗夫与ＩＢＭ公司的国际象棋电脑深蓝的6局对抗赛就是计算机用了穷举法战胜了人类。

2016年人类展开了一次，可以写入历史的“人机大战”。这场大战持续了5天，受到了全世界的关注，比赛一方是谷歌阿尔法狗，另一方是世界围棋冠军，韩国名将李世石，九段棋王。AlphaGo，是一款围棋人工智能程序，由谷歌旗下公司戴密斯·哈萨比斯领衔的团队开发，主要工作原理是"深度学习"。虽然没有用到穷举法。但是其数据结构依然是邻接矩阵。

附计算机运算过程控制台输出文件：控制台输出的运算过程