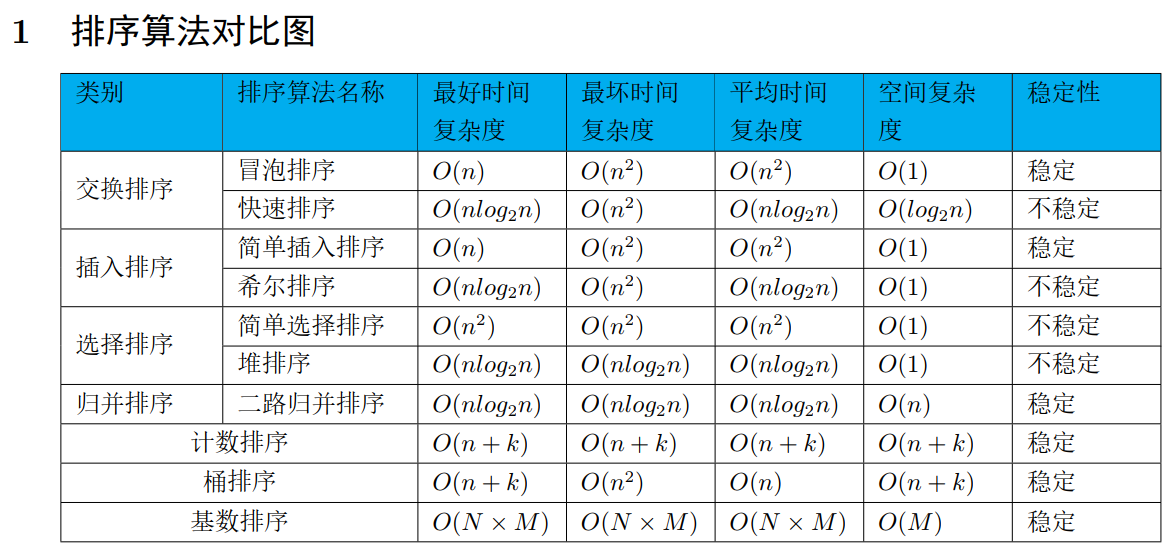
经典排序算法的复杂度对比图表
1527 2025-01-08 23:05 2025-01-09 11:29
对于 \(O(n \log n)\)、\(O(n)\) 和 \(O(n + k)\) 这三个时间复杂度,我们需要根据具体的情况来比较它们的大小:
- 当 \(k\) 很小,即 \(k\) 远小于 \(n\) 时,\(O(n + k)\) 接近于 \(O(n)\),此时 \(O(n)\) 和 \(O(n + k)\) 都比 \(O(n \log n)\) 小。
- 当 \(k\) 很大,即 \(k\) 接近于 \(n\) 或大于 \(n\) 时,\(O(n + k)\) 接近于 \(O(2n)\) 或更大,此时 \(O(n + k)\) 比 \(O(n)\) 大,但仍然可能比 \(O(n \log n)\) 小,具体取决于 \(n\) 和 \(k\) 的具体值。
因此,没有一个绝对的答案,需要根据 \(n\) 和 \(k\) 的具体值来确定。但在一般情况下,如果 \(k\) 不是特别大,\(O(n)\) 和 \(O(n + k)\) 都比 \(O(n \log n)\) 小。如果 \(k\) 非常大,那么 \(O(n + k)\) 可能比 \(O(n \log n)\) 大。
所以,如果 \(k\) 不是特别大,那么 \(O(n)\) 和 \(O(n + k)\) 都比 \(O(n \log n)\) 小,而 \(O(n)\) 和 \(O(n + k)\) 的大小则取决于 \(k\) 的值。如果 \(k\) 非常大,那么 \(O(n + k)\) 可能比 \(O(n \log n)\) 大。
一般,O(1) < O(n) < O(nlogn) < O(n^2)
非线性时间比较类排序和线性时间非比较类排序是排序算法的两大类,它们的主要区别如下:
### 非线性时间比较类排序
- **定义**:这类排序算法通过比较元素之间的大小关系来决定它们的相对次序。常见的算法包括冒泡排序、快速排序、归并排序、堆排序等。
- **时间复杂度**:其时间复杂度不能突破 \(O(n\log n)\),因此称为非线性时间复杂度。
- **特点**:在排序过程中,每个元素都需要与其他元素进行比较,以确定其在排序序列中的位置。
### 线性时间非比较类排序
- **定义**:这类排序算法不通过比较元素之间的大小关系来决定它们的相对次序。常见的算法包括计数排序、基数排序和桶排序。
- **时间复杂度**:可以突破基于比较排序的时间下界,以线性时间 \(O(n)\) 运行。
- **特点**:通常利用了输入数据的某些特性(如数字的位数、范围等)来进行排序。例如,计数排序通过统计每个元素出现的次数来确定其位置。
### 总结
- **排序方式**:非线性时间比较类排序依赖于元素之间的比较,而线性时间非比较类排序则不依赖于比较。
- **时间复杂度**:非线性时间比较类排序的时间复杂度为 \(O(n\log n)\),而线性时间非比较类排序的时间复杂度为 \(O(n)\)。
- **适用场景**:非线性时间比较类排序适用于一般的排序场景,而线性时间非比较类排序适用于具有特定特性的数据集(如数据范围较小或数据分布均匀)。

全部评论